GMorse Part 1 - Project Layout

October 4, 2025

If you made here, I’m assuming you’re at least intrigued about what it takes to implement a Morse code decoder. This is going to be a multi-part article. In this first part I’ll be laying down the foundation of the project, identifying what makes up a functional decoder, and break down the project into different steps.

Introduction to Morse code

So what IS Morse code? You’ve probably at least heard the term before or maybe actually heard some in an old movie or on Youtube. Morse code was invented by Samuel Morse in the first part of the 19th century when he co-developed an electric telegraph system with Josepth Henry and Alfred Vail. The “on”/“off” nature of the telegraph system’s electrical signals made it obvious that establishing a code to transmit natural language over electric wire was necessary. Essentially, Morse code encodes all the letters of the alphabet (and some symbols) into sequences of short and long electrical pulses, seperated by varying lengths of silences. Conventionally, short pulses are referred to as “dits” while long pulses are referred to as “dahs”.

In written form (and throughout these text files), “dits” are represented by “.” and “dahs” by “-”.

Timing

When transmitting Morse code, timing is key. Long pulses (“dahs”) should be three times the length of short pulse (“dits”). Since letters are encoded using a combination of “dits” and “dahs”, the silence between the electrical pulses when transmitting a specific letter or symbol should be the length of a “dit”. Whole letter or symbol transmissions are separated by silences the length of three “dits” (or one “dah”). Finally, words are separated by a silence the length of seven “dits”.

You probably guessed it by now, the absolute reference for all the timing is the length of a single “dit”. But… What should the length of a “dit” be? “dit” seems pretty arbitrary for a unit of meature of time.

Enter “WORDS PER MINUTE”. Words per minute (WPM) dictate the speed at which Morse code is transmitted over a medium (be it a wire, radio frequency, etc). Obviously, the higher the words per minute, the faster the transmition, and subsequently the shorter the length of a “dit”. The WPM is computed from the number of times the word “PARIS” can be transmitted within a minute. The word “PARIS” contains 50 “dits” lengths.

Need proof? Here’s a break down of how to count the number of “dits” in the word “PARIS”. The numbers between parentheses represent the length of silences between pulses. Remember, “dahs” are three times the length of a “dit”, space between pulses is a single “dit”, space between characters is three “dits”, and finally space between words is seven “dits”.

P = .--. = 1 (1) 3 (1) 3 (1) 1 (3) = 14.  
A = .-   = 1 (1) 3 (3)             = 8.  
R = .-.  = 1 (1) 3 (3) 1 (3)       = 10.  
I = ..   = 1 (1) 1 (3)             = 6.  
S = ...  = 1 (1) 1 (1) 1 (7)       = 12.  

Total = 50.

A total of 50 “dits” in length. The length of a “dit” for a single “PARIS” word can be calculated by dividing 60 (seconds) by the number of “dits”: 50 in this case. The resulting ratio is 60/50. Based on this, computing the length of a “dit” for a given number of words per minute simply becomes 60 / (50 * wpm).

So, to give an example, at 15 wpm, the timing of a transmission would result in a single “dit” being ~80 milliseconds.

Tone Frequency

Morse code is nothing more than a series of pulses and silences. I don’t know about you, but I cannot hear electrical pulses, and I cannot see radio frequencies either. When transmitted for human interpretation, Morse is transformed into a single audible tone that is usually set to 700Hz, but can be anywhere between 500Hz and 900Hz. This “tone” is actually a sine wave at a specifically selected frequency. Note that Morse is also refered to as “Continuous Wave” (CW for short) because of this.

Wraping up Morse code

In a hurry? here’s the TL;DR.

Morse code is defined by a pulsating signal. Letters and symbols are encoded into a series of short (“dit”) and long (“dah”) pulses surrounded by silences. In the specific case of Morse code carried in an audio signal, the pulses are represented by a single audible tone (CW) between 500Hz and 900Hz.

Timing is also a crucial part of the encoding and decoding process. The shortest pulse (“dit”) is used as a reference for all the other lengths of pulses and silences that compose the different encodings for character. The length of the short pulse is dictated by the transmission speed, described as words per minute (WPM) and can be calculated by dividing 60 (seconds) by 50 * WPM (transmission speed).

This information lays down the foundations for the requirements of the Morse decoder project. Next up is breaking down the problem into steps that can done independently and then assembled to make a whole.

Breaking Down The Problem

Breaking down the problem into manageable pieces with clear milestones is crucial. At least for me. Anything too large or complex gets abandonned pretty quickly, either out of boredom or lack or tangible progress. That’s why I spend some time figuring out a plan before I even start writing down some code. Part of the research and learning is done in this phase as well.

Anyway, going over it again, I know I’ll be working with a sampled analog signal, essentially “digitized”. This is a fact, simply because the radio is hooked up to my laptop through USB and appears as a USB audio device. Once audio is sampled, I need to figure out how to detect the Morse code tone in it. Morse is a continuous wave between 500Hz and 900Hz, that’s where the tone detection effort will be focused. After that, when tone is detected, I can then move forward to measure the length when the tone is present and when it’s not. Based on the timed nature of Morse code, the next step will be building a Morse decoder to do the interpretation of the presence of the tone and silences to determine what character was received.

High level, this sounds pretty simple but did require a good math refresher for the tone detection part and creative uses of binary trees for the decoding part. Here’s a rough schema of how everthing will be hooked up together.

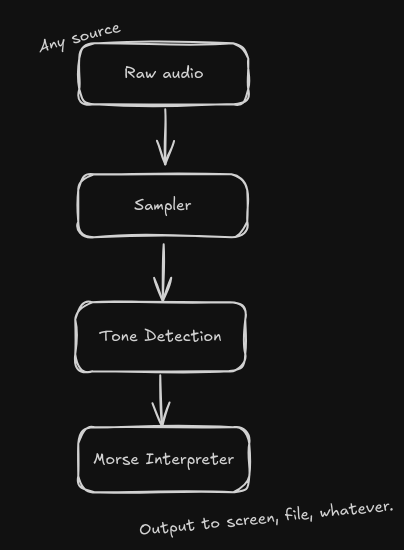
Conclusion

This concludes part 1. What I covered up until now is really just understanding what Morse code and Continuous Wave (CW) are along with their specifications. I outlined of what needs to be done and put together in order to make a computer decode Morse code from an audio source. Every part of this article series will tackle each “box” in the project schema presented above. I’ll go over the research done and provide a link to the code on my Github that resulted in putting that piece of the puzzle together.

Thanks again for reading! Hope to see you in part 2!

-redbay